Čuvene matematičke jednačine koje bi svako trebalo da zna

Sagledajte svet kroz devet matematičkih teorija koje su revolucionisale ljudsko znanje, od Pitagorine teoreme do teorije haosa. Otkrijte vašu ljubav prema matematici.

Ono što znamo je kap, a ono što ne znamo je okean.

Isak Njutn

Formule zauzimaju središnje mesto u ogromnom matematičkom univerzumu. Ove čuvene jednačine se nalaze u svakoj matematičkoj teoremi od drevnih vremena do otkrića u dvadesetom veku. Svaka nova matematička jednačina, donosi veliki broj novih pitanja, a novi odgovori se pojavljuju.

Sledi antologija nekih matematičkih jednačina, koje su promenile način na koji sagledavamo svet.

Želiš da držiš časove?

Pridruži se zaјednici Superprof i podeli svoјe znanje sa stotinama radoznalih i motivisanih učenika

Kreiraj oglas

Pitagorina teorema

Ova teorema koja potiče iz 530-te godine pre Hrista, je verovatno najpolularnija matematička jednačina koja postoji.

Evo formule:

a² + b² = c²

Pitagorina teorema je jedna od kamena temeljaca moderne matematike. Dala je značajan doprinos razvoju matematike kao discipline. Formula ove teoreme ostaje ukorenjena u vašem pamćenju, čak i posle mnogo godina.

Zahvaljujući Pitagori i njegovoj čuvenoj jednačini, možemo da lako izračunamo dužine, uglove i da odredimo da li je trougao pravougli ili ne. Ova jednačina je samo jedna od brojnih primera da je matematika deo našeg svakodnevnog života, bili mi svesni toga ili ne.

Pitagorina teorema se i dalje koristi na praktičnim poljima, poput izgradnje, arhitekture i u stolarskom zanatu, pored ostalih.

Univerzalni zakon gravitacije

Ova sila je direktno proporcionalna proizvodu masa tela i indirektno proporcionalna kvadratu razdaljine između njih.

Na primer, Zemlja privlači Mesec, i obrnuto.

Isti, Univerzalni zakon gravitacije se odnosi na privlačnost između jabuke i Zemlje, i na privlačnost između planeta i Sunca.Ovaj zakon i jednačinu, jednu od najčuvenijih matematičkih jednačina koje postoje, je stvorio Isak Njutn. Formulisao je u sedamnaestom veku. Formula je sledeća:

F = G(m₁m₂)/R²

U kojoj je:

• F: Gravitaciona sila (N: Njutni)
• m₁: Masa prvog tela (obično planete, kilogrami)
• m₂: Masa drugog tela (kilogrami)
• r: Razdaljina između tela (metri)
• G: Gravitaciona konstanta

Gravitaciona interakcija je univerzalna. Ona se primenjuje na sve tipove materije. I gravitacija se isključivo manifestuje kao privlačna sila; ona ne uzima u obzir odbijanje tela.

Teorija relativnosti

Čista matematika je, na svoj način, poezija logičnih ideja.

Albert Ajnštajn

Formula teorije relativnosti je sigurno jedna od najčuvenijih formula koje postoje. A ipak, niko je u potpunosti ne razume.

Teoriju relativnosti je razvio Albert Ajnštajn, koji je pomogao u revolucionisanju naučnog razumevanja prirode prostora i vremena.

Ovo je jedna od najčuveniji matematičkih teorija, a njena formula je:

E = mc²

Ali na šta se ova formula odnosi?
Prvo, važno je napomenuti kako je masa bilo kog objekta oblik energije. U fomuli, masa (m) objekta može biti pretvorena u energiju (E) i obrnuto. Slovo „c“ predstavlja brzinu setlosti, i ona je podignuta na kvadrat da bi se istaklo kako čak i mala količina mase može biti preobražena u veliku količinu energije.

E predstavlja energiju, m masu tela, a c brzinu svetlosti.

Ograničena relativnost uvodi ideju da je brzina svetlosti univerzalna konstanta koja se ne menja, i da prolazak vremena nije isti, za tela koja se kreću različitim brzinama.

Teorija relativnosti je najčuvenija metamatička teorija na svetu, zato što je dokazala kolika je važnost matematike u stvarnom životu i koliki uticaj može da ima na tok istorije.

Želiš da držiš časove?

Pridruži se zaјednici Superprof i podeli svoјe znanje sa stotinama radoznalih i motivisanih učenika

Kreiraj oglas

Teorija haosa

Teorija haosa je nauka neočivanog, nelinearnog i nepredvidljivog. Ona je jedna od najčuvenijih matematičkih teorija.

Ova teorija se bavi nelinearnim fenomenima koje je praktično nemoguće predvideti ili kontrolisati, kao što su turbulencija, vremenske prilike, berze, stanja mozga, i tako dalje. Ovi fenomena, koji odražavaju beskrajnu složenost prirode.

Teorija haosa obuhvata, na primer, efekat leptira. Ovaj efekt se često opisuje na sledeći način: leptir koji zaleprša krilima u Australiji, može da izazove uragan u Čileu. Ona možda zvuči kao fantazija, zar ne? Međutim, teorija haosa dozvoljava postojanje ovog efekta. Preciznije, efekat leptira znači da male promene u inicijalnim uslovima, mogu da dovedu do drastičnih promena u ishodima.

Naši životi su neprestana demonstracija ovog principa. Pošto nikad ne možemo znati sve inicijalne uslove kompleksnih sistema, dovoljno detaljno, ne možemo očekivati da predvidimo njegov ishod. Ovo može biti u direktnoj suprotnosti s našom idejom da koristimo matematiku za poker ili kockanje, pošto će čak i male greške u merenju stanja sistema biti veoma pojačane, čineći svako predviđanje beskorisnim. Ovo je jedna od najzanimljivijih matematičkih teorija.

Haos je došao u fokus šezdesetih godina dvadesetog veka, kad je meterolog Ed Lorenc pokušao da napravi osnovnu kompjutersku simulaciju zemljine atmosfere.

Haos je dospeo u žižu javnosti 1960-ih godina, kada je meteorolog Ed Lorenc pokušao da napravi osnovnu kompjutersku simulaciju Zemljine atmosfere.

Ojlerov identitet

Ojlerov identitet je dat u sledećoj jednačini:
eiπ = −1

Veliki broj matematičara i stručnjaka smatra da je ova jednačina jedna od najčudesnijih koje su ikad stvorene.

Ne samo zbog svoje elegancije, već i zato što povezuje pet važnih matematičkih konstanti u jednoj formuli:

• e: baza prirodnog logaritma
• i: imaginarna jedinica
• π: 3,1416
• 1 i 0: celi brojevi

Elegancija Ojlerovog identiteta leži u njenoj jednostavnosti.

💡Ona, zahvaljujući njenoj jednostavnosti, utiče na oblasti kao što su inžinjerstvo, teorija brojeva i kompleksnih funkcija, između ostalih.

Šredingerova jednačina

Ova jednačina je jedna od najčuvenijih formula u matematici. Ne, ovog puta ne govorimo o mački; govorimo o još jednoj briljantnoj Šredingerovoj ideji (Nobelova nagrada za fiziku).

Šredingerova jednačina je suštinska za razumevanje kako se čestice menjaju vremenom. Ona nam pomaže u opisivanju različitih stanja u kojima čestice mogu biti pronađene. Ta jednačina, pored tehničke važnosti, postavlja fascinantno filozofsko pitanje: Da li je materija stvarno sastavljena od konkretnih fizičkih stanja, kao što su čvrsto, tečno i gasovito, ili je nešto više u igri? Drugim rečima, ona nas poziva na razmišljanje o pravoj prirodi materije, i o tome kako se je opažamo. Ova vrsta matematičkih enigmi je veoma česta, a ova jednačina predstavlja vrata ka odgovorima, koji će konačno biti pronađeni.

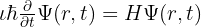
Šredingerova jednačina je bila veoma korisna za unapređenje nuklearne energije, kao i za izračunavanje i primenu lasera.

Zahvaljujući ovoj, jednoj od najčuvenijih matematičkih jednačina u istoriji, smo sposobni da bolje objasnimo ponašanje atoma i subatomskih čestica.

Šredingerova jednačina objašnjava promene na čestici u vremenu. Ona opisuje stanje čestice, iz kog je moguće opisati svako stanje.

Maksvelove jednačine

Četiri Maksvelove jednačine obrazuju jedan od najvažnijih temelja savremene fizike. Ove jednačine su bile veoma značajne za elektrodinamiku i teoriju relativnosti.
Otkriće Maksvelovih jednačina se smatra vrhuncem klasične fizike, pošto sve jednačine elektromagnetizma mogu da se izvode iz njih. Te jednačine opisuju interakciju između električnih i magnetnih polja, i njihov odnos s električnim poljima i naponima. Električna i magnetna polja mogu biti predstavljena. Grafički govoreći, oba predstavljaju ispoljavanje sile na naponima. Jednostavno rečeno, možemo ustvrditi da su električna i magnetnka polja povezana. One stupaju u interakciju jedna  drugima i mogu biti modifikovana.

Čuvene jednačine su silno doprinele matematici. One nisu samo znanje po sebi, već omogućuju stvaranje i unapređenje drugih matematičkih koncepata.

Sve ove čuvene matematičke jednačine imaju nešto zajedničko: One su jednostavne (u pogledu elegancije), koncizne i pomažu u povezivanju fundamentalne matematike sa jednostavnijim konceptima. Svaka od ovih jednačina ima široku i duboku primenu u svakodnevnom životu i raznovrsnim disciplinama, što ih čini tako vrednim. I iako matematika može biti pomalo kompleksna, ona ostaje fascinantna.

Jezik matematike je univerzalan. Nije važno da li govorite engleski, francuski ili španski. Ako razumete jezik matematike, razumeće vas na bilo kom jeziku. Ovaj jezik je načinjen tako da možemo da otkrijemo univerzom koristeći se jednim oblikom komunikacije, jezikom matematike.